DMT: Duration of liabilities
Introduction
DMT stands for Discounted Mean Term and is also known as Macaulay Duration. We often use it in the calculation of the expected average duration of the liabilities.
We use the average duration to ascertain the discount rate used in our Gratuity and Leave Encashment actuarial reports as per AS15, IAS19 and IndAS19, explained in detail in “Application” section below.
Importance
DMT measures the average duration of a liability (Defined Benefit Obligation or DBO liability in this case). Liabilities with higher duration have a higher discounted value and are thus more sensitive to movements in discount rate, and vice-versa.
In a wider context, DMT is also used as an investment risk management tool. Investment managers and/or actuaries may match the duration of assets with duration of liabilities calculated using DMT. This is a part of minimizing interest rate risk strategy, also known as “immunization strategy”.
Formula
We denote DMT using the Greek symbol “τ” (Tau), calculated using the following formula:

Key Features
- DMT is dependent on the interest rate (or discount rate) as well as the amount and timing of cashflows.
- DMT is an average of the timings of a series of cashflows and hence should lie between the timing of the first and the last cashflow.
- For instance, DMT of 8 years implies that:
- On an average, the liability is paid out in the 8th year.
- However, in essence, payments may occur both before and after the 8th year.
- For better understanding, please see the example below where gratuity is paid in the 5th and 10th years respectively, but the DMT is 8 years.
Example
Let us assume that:
- We pay
- ₹2 lakhs Gratuity (C) to an employee resigning after 5 years (t) of service.
- ₹5 lakhs Gratuity (C) to another employee retiring after 10 years (t) of service.
- The effective discount rate (i) is 10% p.a.
Using the formulae above, we calculate:
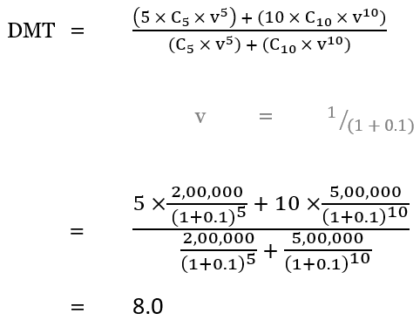
Therefore, the duration of liability (or DMT) is 8 years.
Application
The liabilities for both Gratuity and Leave Encashment schemes are valued as per Indian accounting standards (IndAS19 or AS15). The accounting standards prescribe that “the assumption for discount rate must be in accordance with the duration of liabilities of the organization at the date of valuation”.
We use the DMT formula above to calculate the average duration of liabilities and ascertain the discount rate using the following process:
- For each employee, we first calculate probability-weighted cashflows expected for each future time period as per the respective scheme rules (i.e., Gratuity or Leave Encashment).
- Using these cashflows, we then calculate the DMT for each employee.
- We then average the DMT of all employees to calculate the duration of liability of the respective scheme.
- As a last step, we use the duration calculated above to ascertain the corresponding discount rate on the zero-coupon risk-free INR yield curve.
- This is in line with the accounting standards for actuarial valuation of gratuity and leave encashment schemes.
- For the above, we source the risk-free zero-coupon yield curve for Indian Rupee (INR) from CCIL website.
- The above is an iterative process and our software uses our proprietary AI algorithm for this.
